Computer Science Fundamentals
Welcome!
Girl Develop It is here to provide affordable and accessible programs to learn software through mentorship and hands-on instruction.
- We are here for you!
- Every question is important.
- Help each other.
- Have fun!
Welcome!
Tell us about yourself.
- Who are you - names and pronouns
- What do you hope to get out of this class?
What we'll be covering in this class
- What is an algorithm?
- Intro to algorithmic complexity (how good is an algorithm)
- Big O notation
- Analyzing Arrays
Expectations
- Participation and questions
- Positivity
Not expecting:
- Syntax
- Knowing all the things
Algorithms
"A repeatable process for determining the solution to a problem."
Algorithms in Daily Life
Some problems that we can create algorithms for (not necessarily related to computers)
- Finding a fruit in the grocery store.
- Alphabetizing name tags.
- Finding keys that you lost.
- Finding something good to watch on TV.
- Deciding on a place to eat lunch.
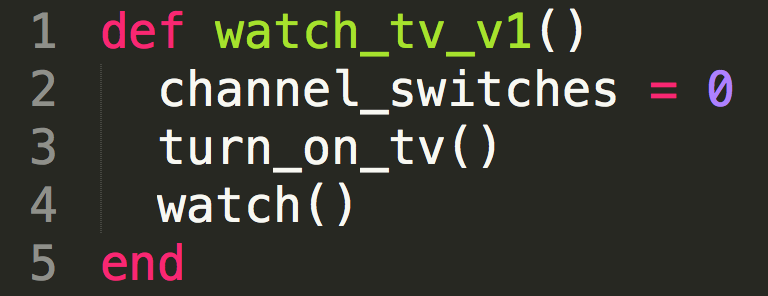
Finding something to watch on TV v1
- Turn on TV
- Watch what is on
Finding something to watch on TV v2
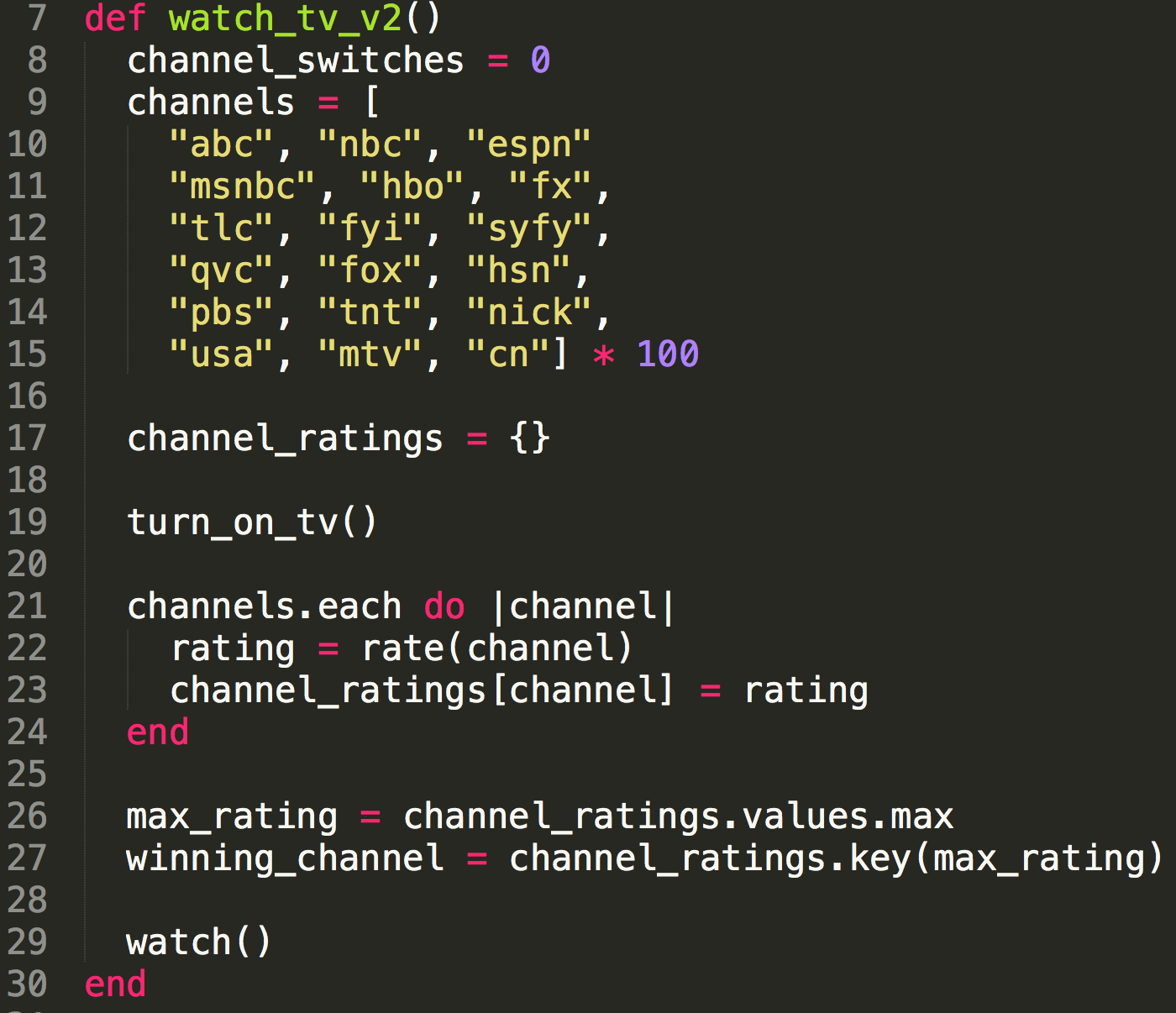
- Turn on TV
- Flip through every channel and rate what is on
- Find the highest rated channel
- Watch
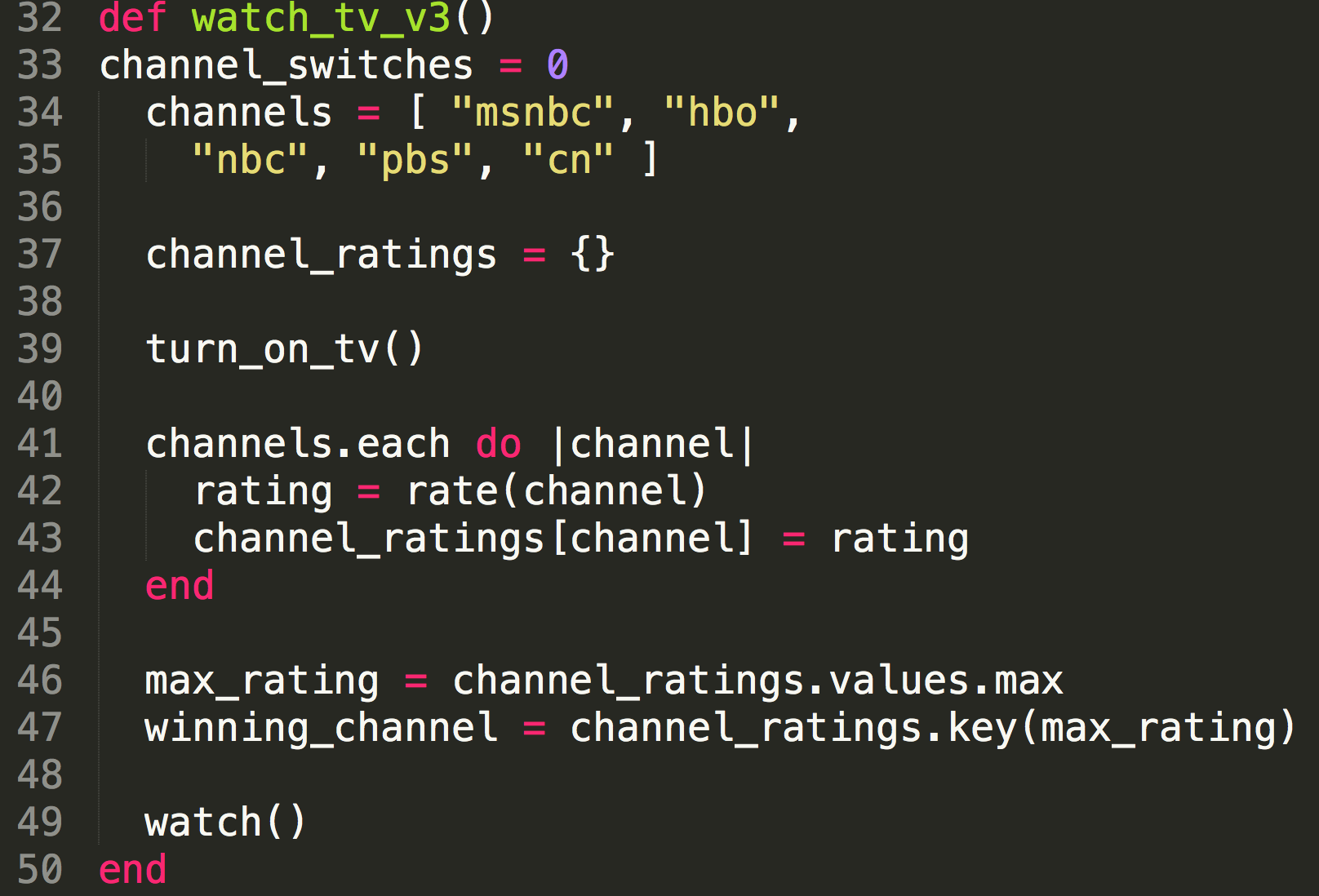
Finding something to watch on TV v3
- Turn on TV
- Check 5 favorite channels and rate what is on
- Find the highest rated channel
- Watch
Which version is best?
Turn on the TV
Rate all channels
ORRate top channels
Goal of Algorithms
- Solve a problem
- in a repeatable way
Exercise time!
What is an algorithm you use?
Find a partner and pick a problem. Come up with multiple versions of an algorithm and write them down.
Ideas:
- Organizing email
- Deciding what restaurant to eat at
- Finding a paper on your desk
- What to wear today
Optimizations
Designing algorithms is about making decisions. Decisions have trade-offs.
You may want to optimize to complete the task:
- in the shortest time
- using the least amount of space
Complexity
How do you know if your algorithm is good?
How do you compare algorithms?
- Time Complexity: How long does the algorithm take
- Space Complexity: How much space does the algorithm use
The less complex the better!
Time Efficient Grocery Shopping
- Drive large car to grocery store
- Buy every thing you need
Saves time, but requires you to have a large car
Lower time complexity
Higher space complexity
Saves time, but requires you to have a large car
Lower time complexity
Higher space complexity
Space Efficient Grocery Shopping
- Walk to grocery store with tote bag
- Buy one item
- Walk home and drop off the item
- Repeat until done
Takes a long time, but doesn't require a car
Higher time complexity
Lower space complexity
Takes a long time, but doesn't require a car
Higher time complexity
Lower space complexity
Time Complexity
How long does an algorithm take?
- Determine how much time each step will take, relative to input size
- Add those times together
- Simplify that expression
Putting Away Laundry v1
- Dump laundry on floor
laundry.drop()
How long does the algorithm take?
Laundry v1
How long does the algorithm take?
Dumping out my laundry takes 2 seconds
| #items | #seconds |
|---|---|
| 4 | 2 |
| 8 | 2 |
| 16 | 2 |
How do we talk about these times more generally for computers?
Big O Notation
- Language we use to describe the complexity of an algorithm
- Approximation of how quickly space or time complexity grows relative to input size
- Usually talking about worst case scenario
- Uses algebra-like notation so complexities are easier to compare
Laundry v1
How long does the algorithm take?
Dumping out my laundry takes 2 seconds
| #items | #seconds |
|---|---|
| 4 | 2 |
| 8 | 2 |
| 16 | 2 |
If N = items of clothing,
time it takes: (N*0 + 2)
Laundry v1 Big O Notation
(N*0 + 2)
→ O(2)
→ O(1)
Constant time
Constant time complexity
O(1) - Big O of 1

where n is the number of pieces of laundry
Laundry v2
- Dump laundry on bed.
- Pick up each piece of clothing, put in a pile for that type ("shirts", "underwear", "socks", etc.)
- After all are in piles, go through each item in each pile, and hang up each one.
Laundry v2 Code
piles = {'shirts': [], 'socks': []}
for clothing_item in laundry:
piles[clothing_item.type].append(clothing_item)
for pile in piles:
for clothing_item in pile:
clothing_item.hang_up()
Laundry v2
How long does the algorithm take?
Putting an item in a pile takes 10 seconds.
Hanging an item up takes 30 seconds.
| #items | #seconds |
|---|---|
| 4 | (4*10 + 4*30) = 160 |
| 8 | (8*10 + 8*30) = 320 |
| 16 | (16*10 + 16*30) = 640 |
If N = items of clothing,
time it takes: (N*10 + N*30)
Laundry v2 Big O Notation
(N*10 + N*30)
→ O(40N)
→ O(N)
Linear time
Linear time complexity
O(n) or Big O of N

where n is the number of pieces of laundry
Comparing constant and linear time complexity

where n is the number of pieces of laundry
Making Outfits
Making all possible outfit combinations.
For simplicity's sake, assume there are an equal amount of pants and shirts.
pants_pile = ['blue-jeans', 'black-jeans', 'dress-pants', ..., 'white-pants'] // (n items)
shirts_pile = ['white-shirt', 'blue-blouse', ..., 'stripe-shirt'] // (n items)
outfits = []
for shirt in shirts_pile:
for pants in pants_pile:
outfits.append([shirt, pants])
Making Outfits
We must match each shirt with each pair of pants.
Looking at each item takes 2 seconds.
| pants | shirts | calculation | seconds |
|---|---|---|---|
| 4 | 4 | (4*2*4*2) | 64 |
| 8 | 8 | (8*2*8*2) | 256 |
| 1024 | 1024 | (1024*2*1024*2) | 4194304 |
If N = # items of clothing and # items in section,
time it takes: (N*10 + N*30 + N*N*2)
Laundry v3 Big O Notation
(N*10 + N*30 + N*N*2)
→ O(40N + 2N2)
→ O(2N2)
→ O(N2)
Quadratic time

Question Time!
We're going to determine the time complexity of some algorithms
- What is the input N?
- How long does each step take?
What is the time complexity of...
Wait times: skipping to the front of a line
O(1) - Constant
O(n) - Linear
O(n2) - Quadratic
What is the time complexity of...
Wait times: waiting in a line
O(1) - Constant
O(n) - Linear
O(n2) - Quadratic
What is the time complexity of...
Wait times: skipping half of a line
O(1) - Constant
O(n) - Linear
O(n2) - Quadratic
What is the time complexity of...
sorting your books in alphabetical order
O(1) - Constant
O(n) - Linear
O(n2) - Quadratic
Data Structures
A way to store data
so that it can be used as desired
Data Structures + Algorithms
A good way to approach an algorithm is to think about the data structures that you know.
What are their properties, and how can they be used to your advantage?
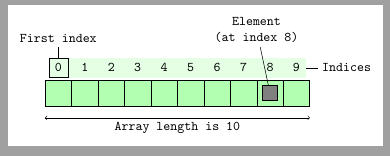
Arrays/List
More questions!
We're going to determine the time complexity of some algorithms
- What is the input N?
- How long does each step take?
What is the time complexity of...
looking up an element in an array
var things = ["raindrops", "roses", "whiskers", "kittens"]
things[2]
O(1) - Constant
O(n) - Linear
O(n2) - Quadratic
What is the time complexity of...
iterating over an array
var things = ["raindrops", "roses", "whiskers", "kittens"]
for (var i = 0; i < things.length; i++) {
things[i]
}
O(1) - Constant
O(n) - Linear
O(n2) - Quadratic
What is the time complexity of...
making every pair combination of items in array
var things = ["raindrops", "roses", "whiskers", "kittens"]
for (var i = 0; i < things.length; i++) {
for (var j = i + 1; j < things.length; j++) {
things[i] + things[j]
}
}
// raindrops + roses
// raindrops + whiskers
// raindrops + kittens
// roses + whiskers
// roses + kittens
// whiskers + kittens
O(1) - Constant
O(n) - Linear
O(n2) - Quadratic
Space Complexity
Time Efficient Grocery Shopping
- Drive car to grocery store
- Get cart
- Put everything in the cart
- Buy items and drive home

The size of the cart grows as the number of items on the list grows.
If N is the number of items on the list, then the cart array needs to be size N.
The space complexity is O(N)

Linear space complexity
O(n) or Big O of N

where n is the number of items on the grocery list
Space Efficient Grocery Shopping
- Walk to grocery store
- Buy first item on list
- Walk home and drop off the item
- Repeat until done
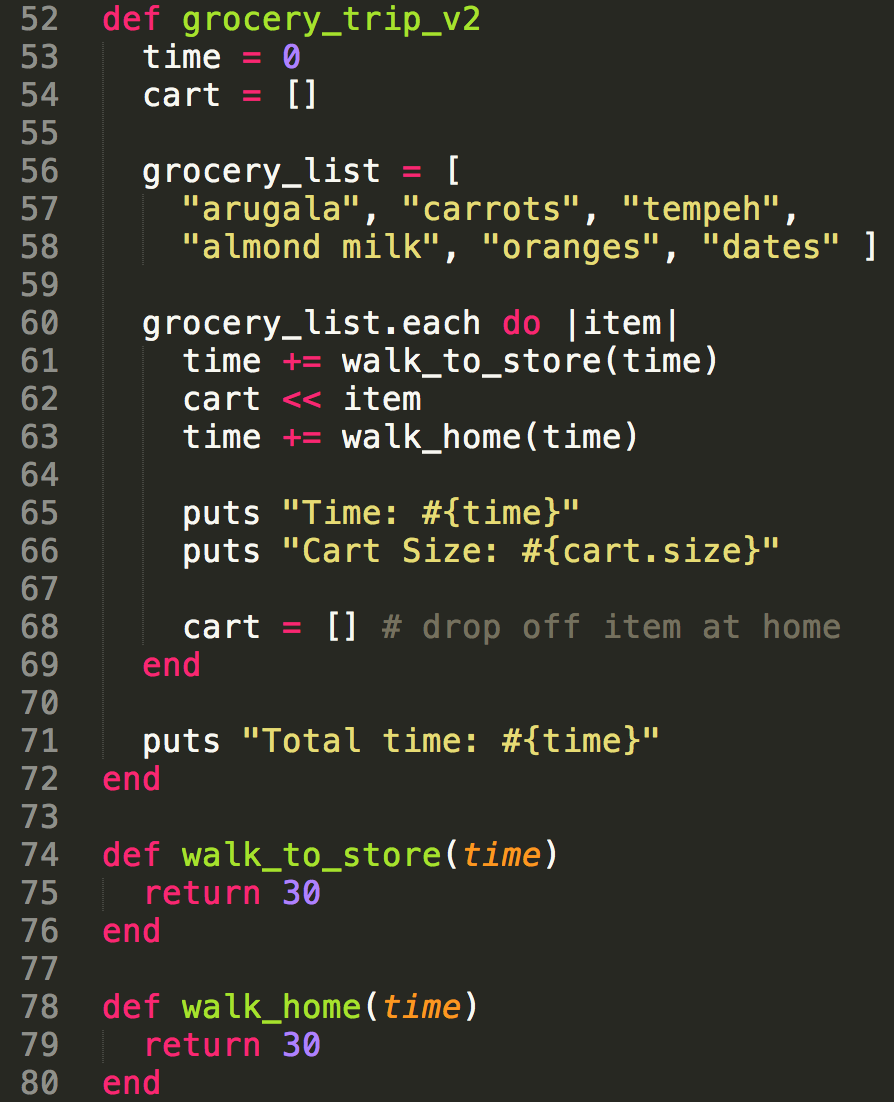
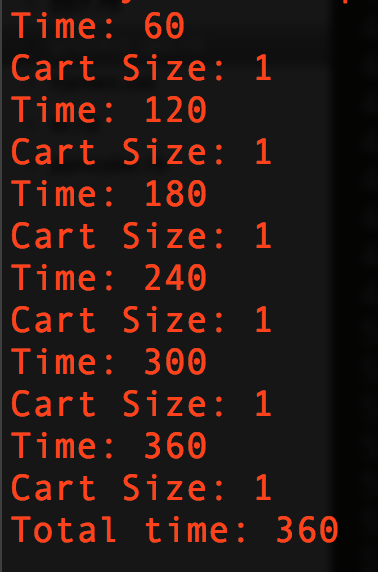
If N is the number of items on the list, then the cart array needs to be size 1.
The space complexity is O(1) or constant.
Constant space complexity
O(1) or Big O of one
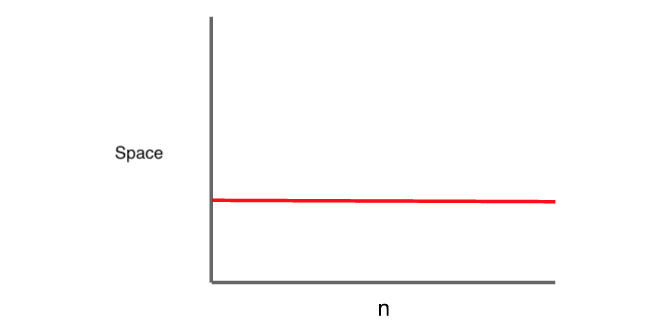
where n is the number of items on the grocery list
What's more important? Time or space?

Discuss!
Refer back to your algorithm from your exercise
What's the time requirement of your algorithm?
What's the space requirement of your algorithm?
Exercise time!
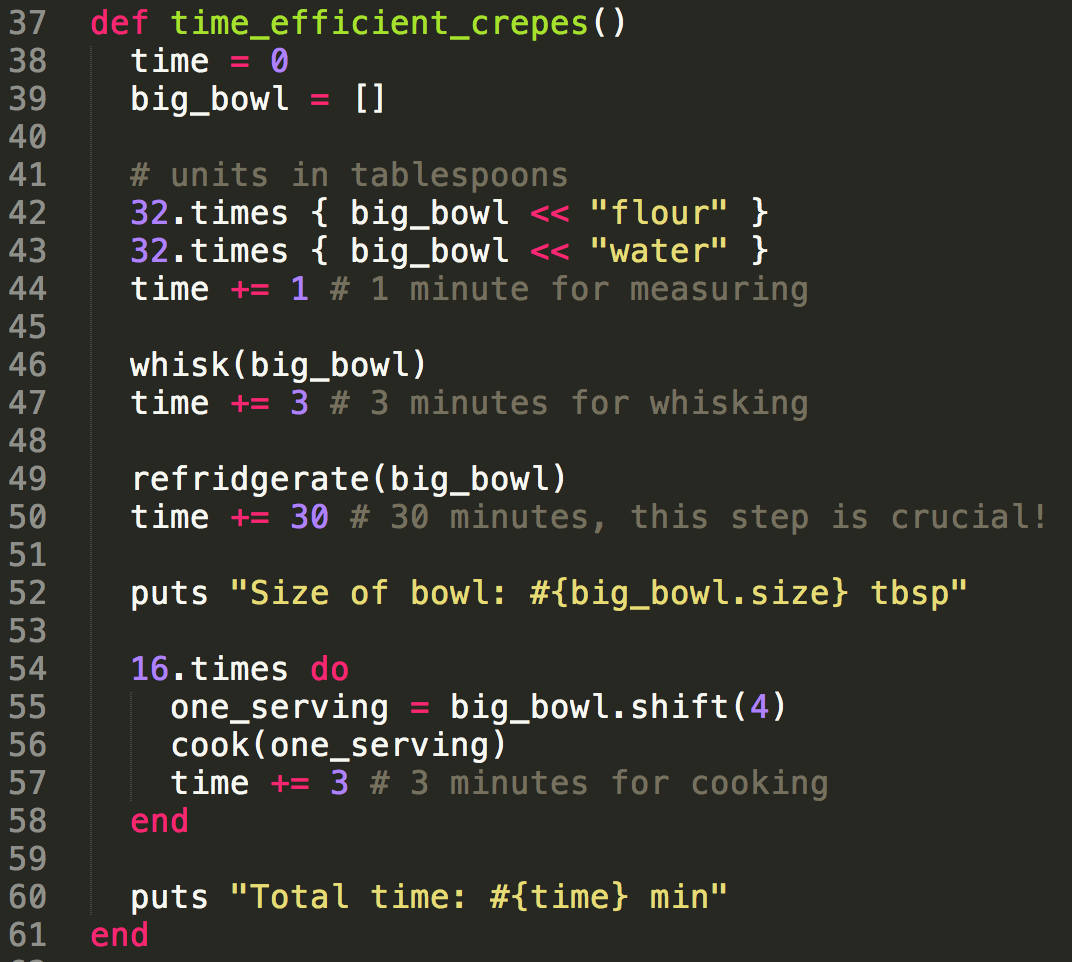
Making Crepes
Write two algorithms for making crepes, one that is time efficient and one that is space efficient.
Pseudocode first then whiteboard code if you have time.

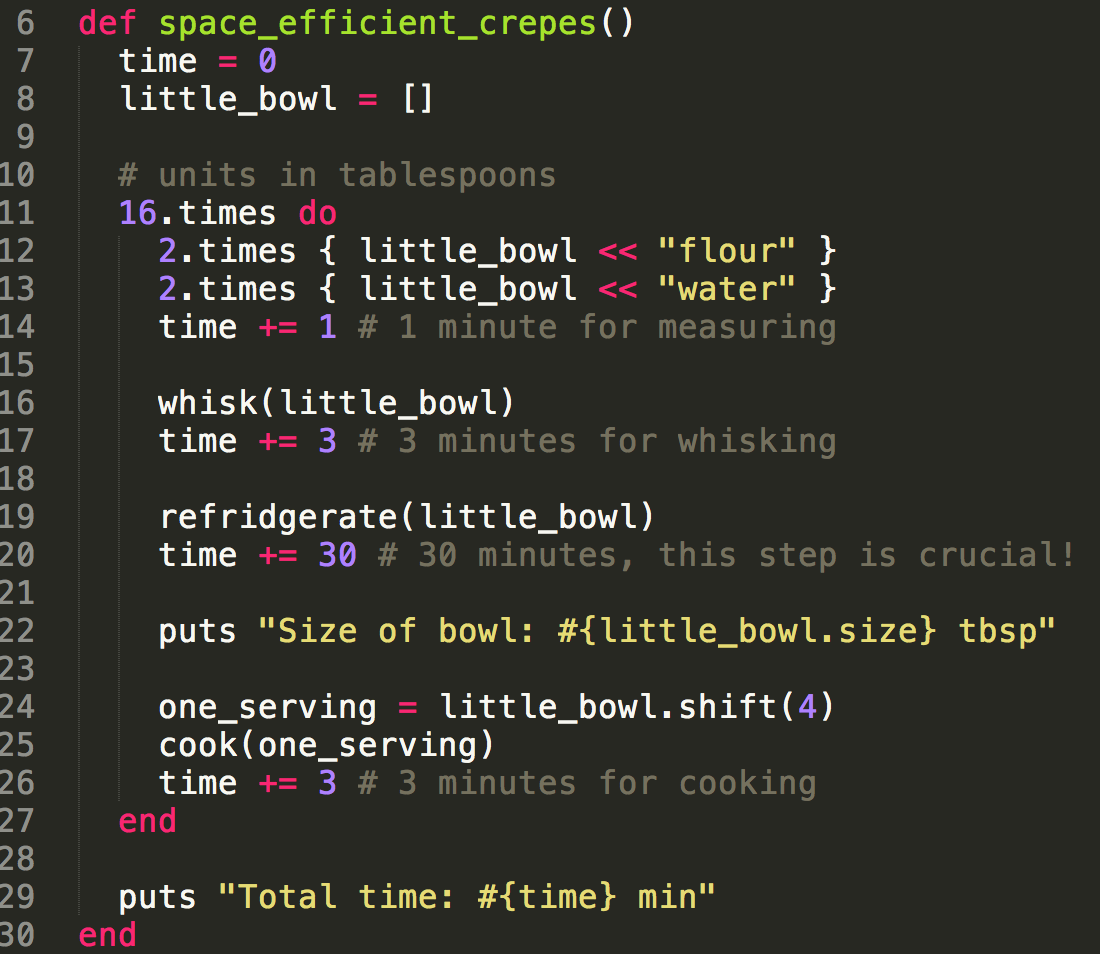
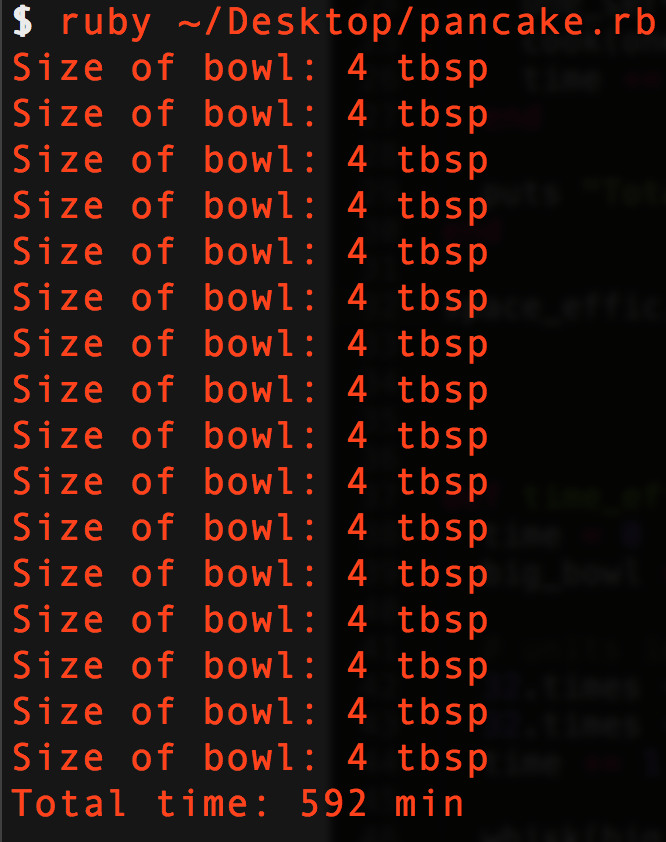
Vocabulary Review
- Algorithm: A repeatable process for determining the solution to a problem
- Time Complexity: How long the algorithm takes
- Space Complexity: How much space the algorithm takes
- Optimization: Making an algorithm take less time or space
- Data Structure: A way to organize data
Time Complexity
| Order of growth | Name | Description | Example |
|---|---|---|---|
| 1 | constant | statement | add two numbers |
| logN | logarithmic | divide in half | binary search |
| N | linear | loop | find the maximum |
| NlogN | linearithmic | divide + conquer | merge sort |
| N2 | quadratic | double loop | check all pairs |
| N3 | cubic | triple loop | check all triples |
| 2N | exponential | exhaustive search | check all subsets |

Abstract Data Structures
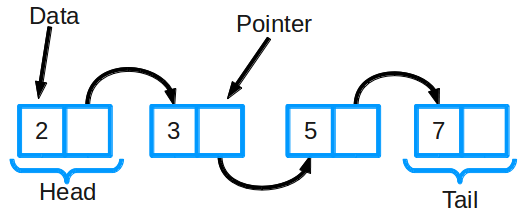
Linked List
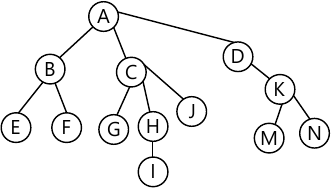
Tree
Graph
Queue
