Searching and Sorting
Searching Algorithms
Search algorithm is an algorithm which solves the problem of retrieving store information.
Wikipedia - Search AlgorithmsDiscuss
How to solve the problem of searching billions pieces of data?

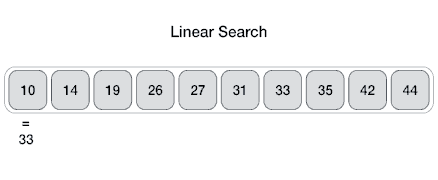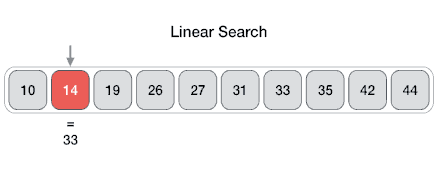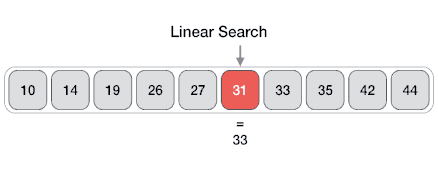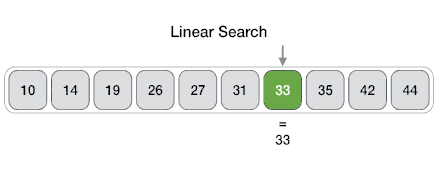
Linear Search
One of the simplest searches.
Find an item with a particular value in a sorted sequence.
Find 'J' in sequence:
[4, 5, J, 10, Q, K, A]
J is the 3rd element (index 2).
Linear Search
Exercise
Writing Linear Search
Click here!
Algorithm Solving Strategies
- Use iteration to move over a data structure
- Use comparison of values
- Use a large, diverse enough data set

Binary Search
Find an item by repeatedly halving the search space.
Binary Search:
Visualized
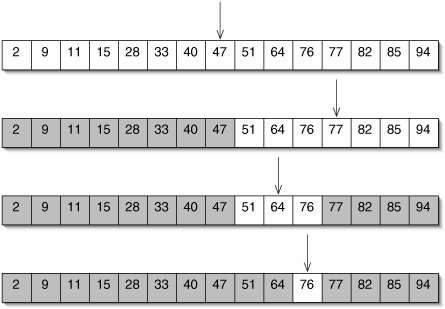
Binary Search: Steps
To find the index of element e with a certain value:
- Start with an array sorted in descending order.
- In each step:
- Pick the middle element of the array m and compare it to e.
- If element values are equal, then return index of m.
- If e is greater than m, then e must be in left subarray. If m is greater than e, then e must be in the right subarray.
- Repeat those steps on new subarray.
Exercise:
Binary Search Simulation
- Sort your cards by number.
- Now let's find a card with a particular number using binary search.
Exercise:
Writing Binary Search
Click here!
Algorithm Solving Strategies
- Use variables as a pointers to 'track' data during an algorithm
- Inside the algorithm, try to make your data set smaller such that you are comparing smaller sets of data to each other - called the 'base case'
Time/Space Complexity
Binary Search vs Linear Search:
What factors determine time?
N = number of items in sequence.
Since binary search algorithm splits array in half every time, at most log2N steps are performed.

Other Searching Algorithms
Performance varies depending on sequence characteristics (distribution)
Sorting
Wikipedia list of sorting algorithsmSorting
Why so important?
You do it all the time in real life
- The way your clothes are organized
- Where your dishes are in the kitchen
- Your books on your bookshelf
They're not in perfect order, but in a way that makes it easier for you to search for things
Sorting
Many sorting algorithms for many types of data
- I sort my dishes by size and shape, not alphabetically
- I sort my books alphabetically, not by color
- I sort post-its in reverse chronological order
- When I sort my yarn I dump them all over the ground
- When I sort my dishes I pull them out of the diswasher one at a time
There are lots of different types of data computers need to sort, just like in the real world

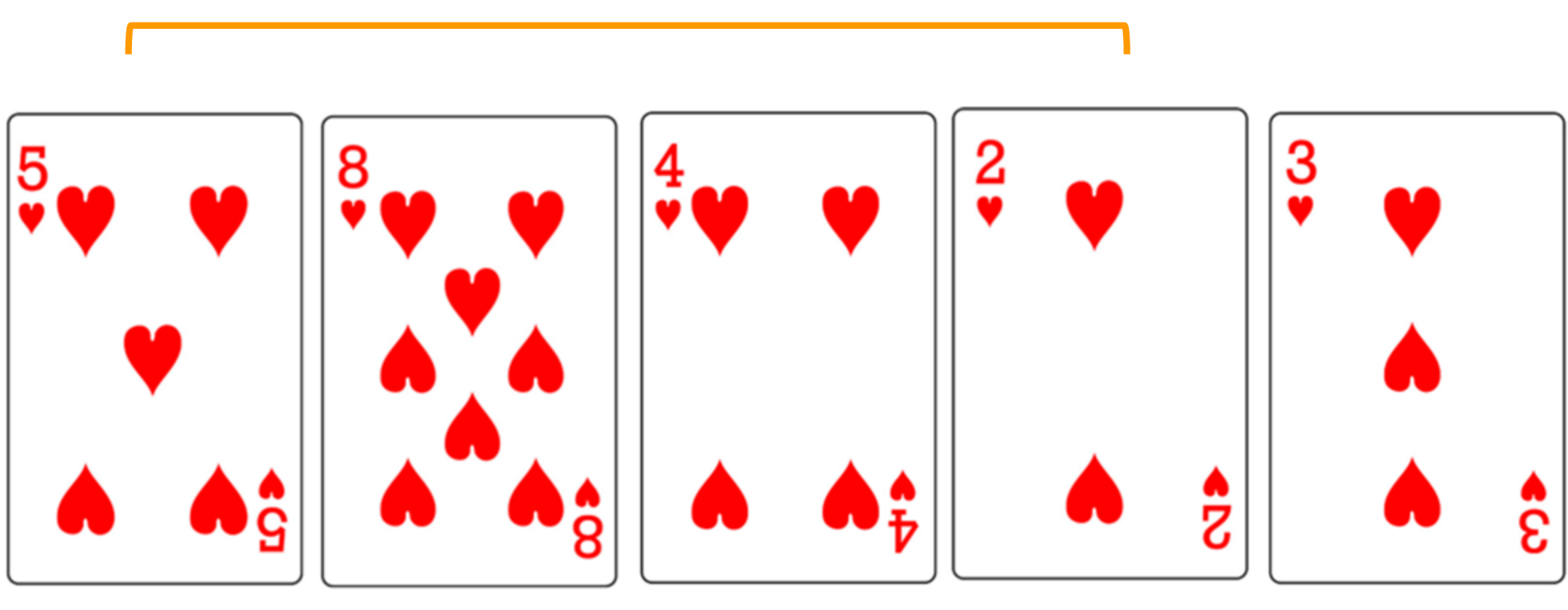
Selection Sort
- Iterate over the unsorted array, keeping track of the minimum value as you go
- When you get to the end of the array, you know which element is the minimum
- Swap the minimum element and the first element in the unsorted array
- The first element is now considered sorted
- Repeat until the rest of the array is sorted
- Find minimum
- Swap in front
- Repeat with unsorted

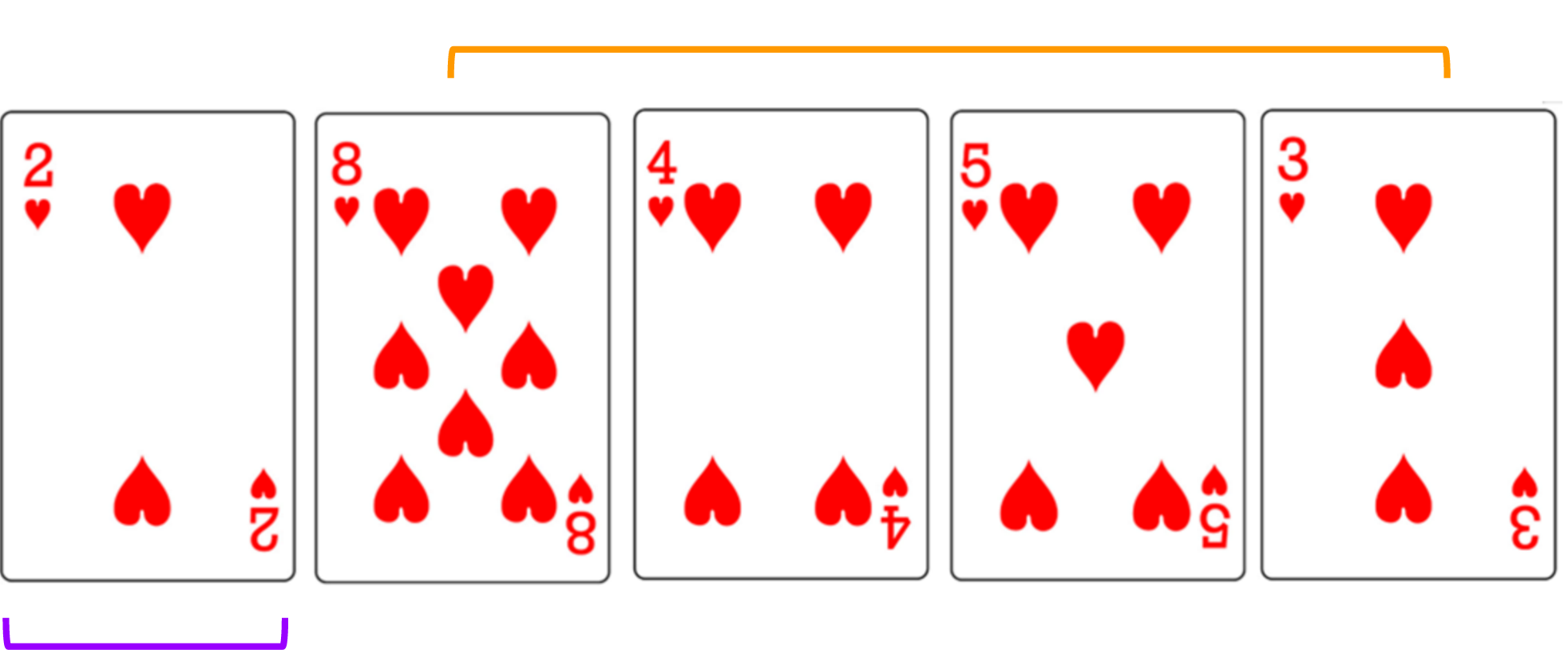
- Find minimum
- Swap in front
- Repeat with unsorted
- Find minimum
- Swap in front
- Repeat with unsorted
- Find minimum
- Swap in front
- Repeat with unsorted
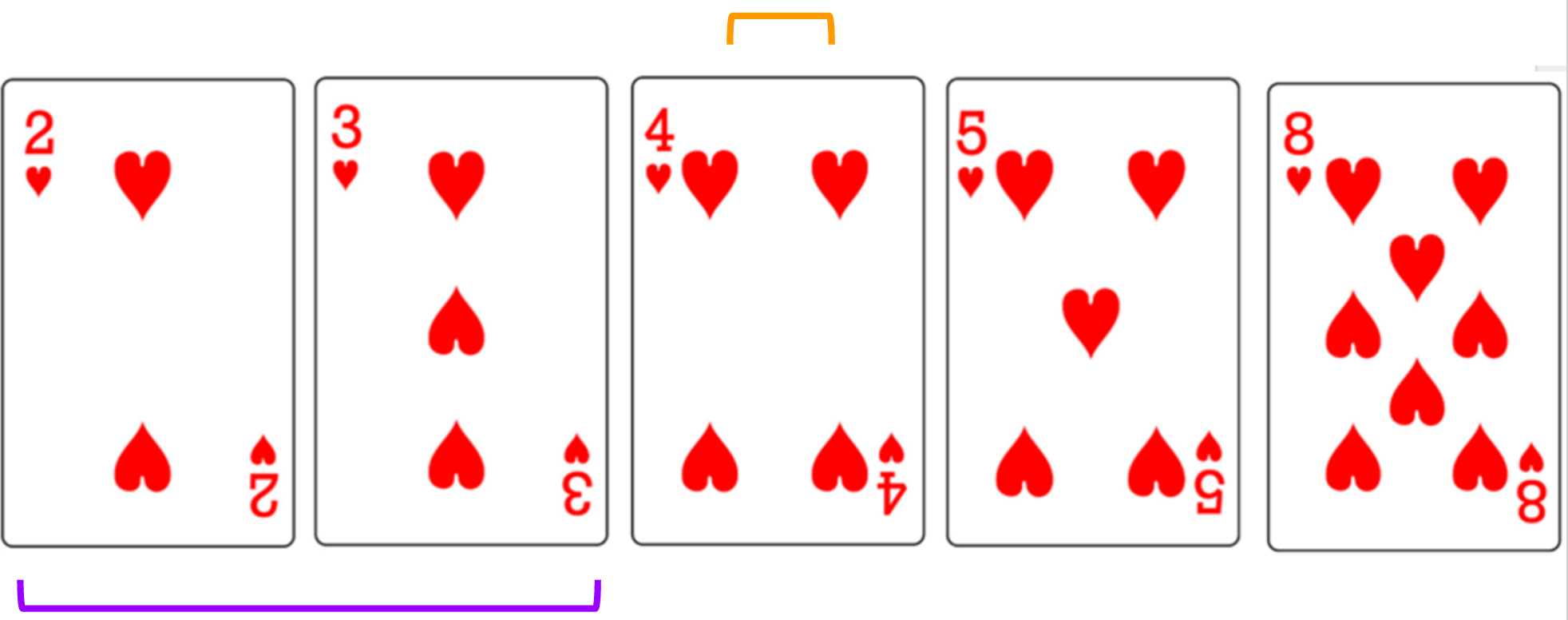
- Find minimum
- Swap in front
- Repeat with unsorted
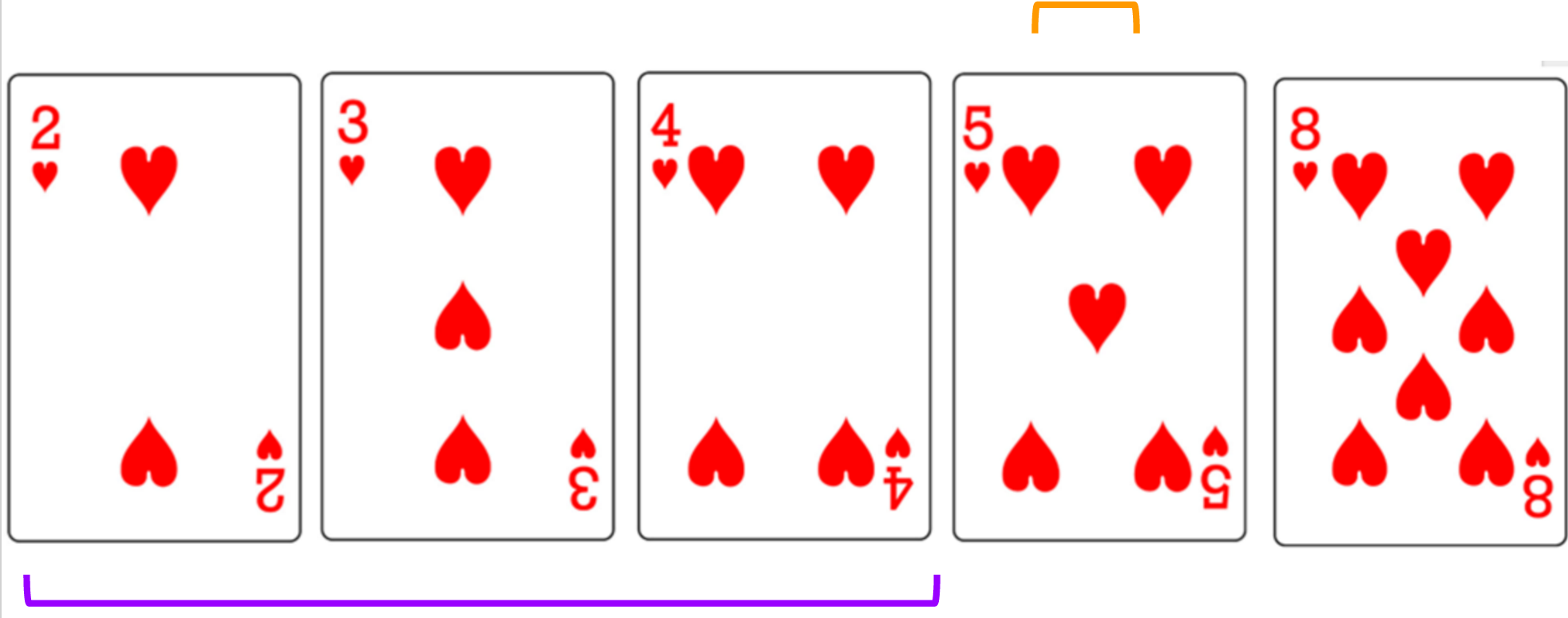
- Find minimum
- Swap in front
- Repeat with unsorted
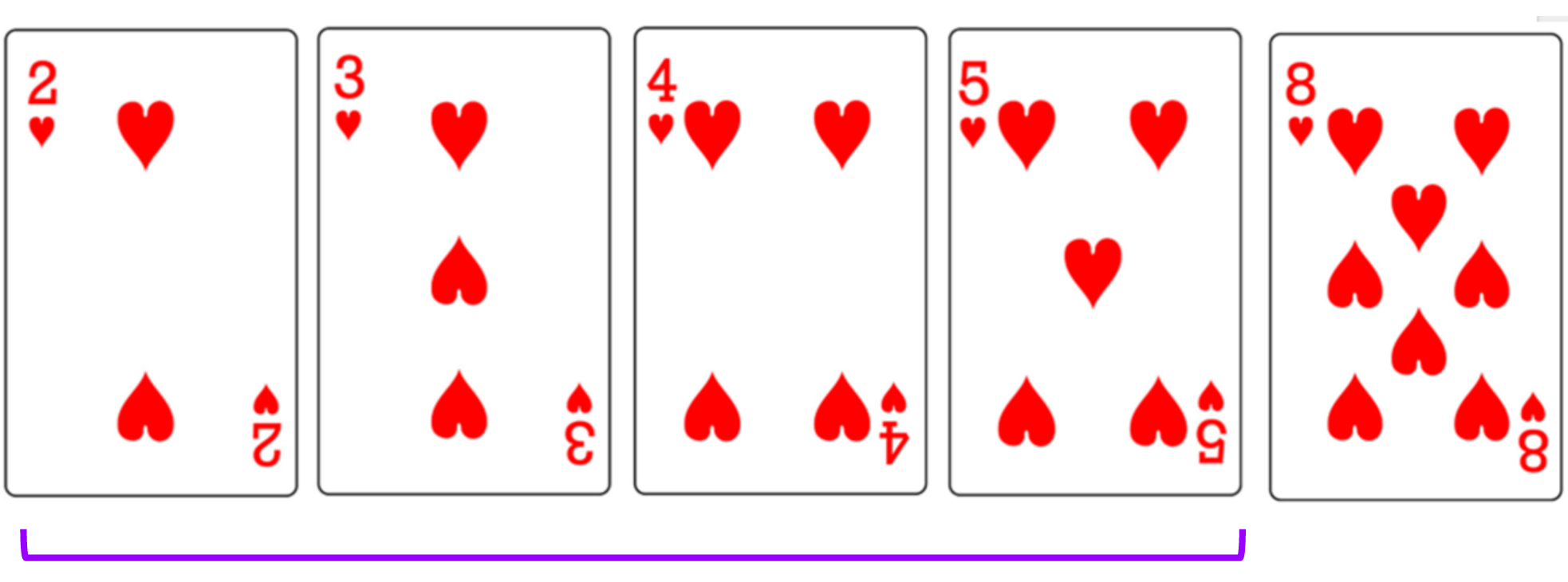
- Find minimum
- Swap in front
- Repeat with unsorted
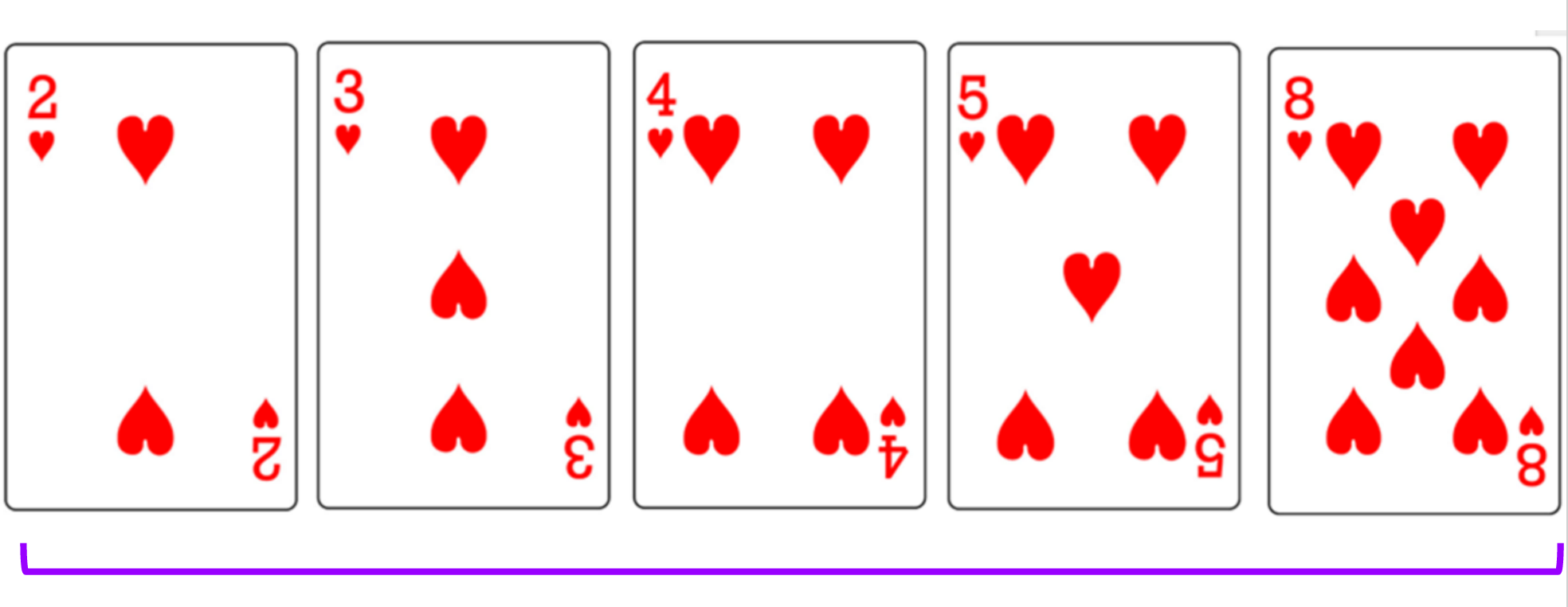
Selection Sort Code
function swap(array, i, j) {
var temp = array[i];
array[i] = array[j];
array[j] = temp;
}
function selectionSort(array) {
for(var i = 0; i < array.length; i++) {
var min = i;
for(var j = i + 1; j < array.length; j++) {
if(array[j] < array[min]) {
min = j;
}
}
if(i !== min) {
swap(array, i, min);
}
}
return array;
}
Selection Sort:
Time Complexity
What is the best case?
What is the worst case?
They are the same! No matter what, selection sort has a time complexity of O(N^2)
Selection Sort:
Space Complexity
Only requires 1 extra temporary variable. O(1)

More Sort Algorithms
All differ in performance, and performance often depends on data characteristics.
Wikipedia: Comparison of algorithm performance, Sorting Algorithms Visualization
Which sort is best?
A great resource to help visualize the different sorting algorithms:
Visualgo.netInsertion Sort
When is it best?
- Good for incremental sorting.
- When you need elements sorted, but you only get them a few at a time
- You run a calendar app. People insert events into the app one at a time and you need to sort the events
Bubble Sort
When is it best?
- When you are in computer science class
- When the values are mostly sorted
Merge Sort
When is it best?
- When you are combining already sorted arrays
- Two companies are merging and they each have seniority lists based on hire dates. They need to combine these lists into one sorted list.
What if...
You have 6 stacks of mostly sorted papers. How would you sort them all together?
- Use bubble sort or selection sort to sort each pile
- Use merge sort to combine the sorted piles
Explore more!
I focused on which type of data is good or bad for each sorting example, but each sorting algorithm also has its own space trade offs as well.
- Quick Sort
- Quick3 Sort
- Heap Sort
- Shell Sort
Searching with other data structures
Matrices
Arrays of arrays
Exercise
Linear search for matrices
Find maximum element of each row in a matrix
Input : [1, 2, 3]
[1, 4, 9]
[76, 34, 21]
Output :
[3, 9, 76]
Input : [1, 2, 3, 21]
[12, 1, 65, 9]
[1, 56, 34, 2]
Output :
[21, 65, 56]
Searching with matrices
What is the time complexity?
O(n*m)
What is the space complexity?
O(n)
Linked Lists
Linked Lists
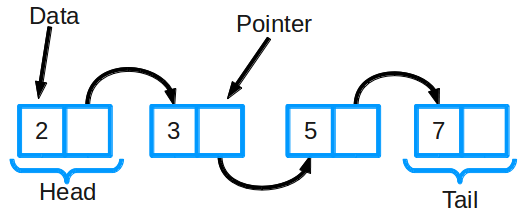
Linked list implementation
class Node(object):
def __init__(self, data=None, next_node=None):
self.data = data
self.next_node = next_node
def get_data(self):
return self.data
def get_next(self):
return self.next_node
def set_next(self, new_next):
self.next_node = new_next
Exercise
Writing find max with Linked Lists
Click here!
Complexity of linked lists
WikipediaOther searching and sorting
Trees - breadth first and depth first search
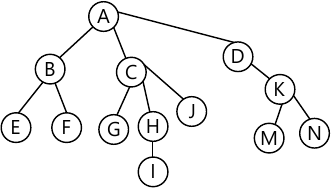
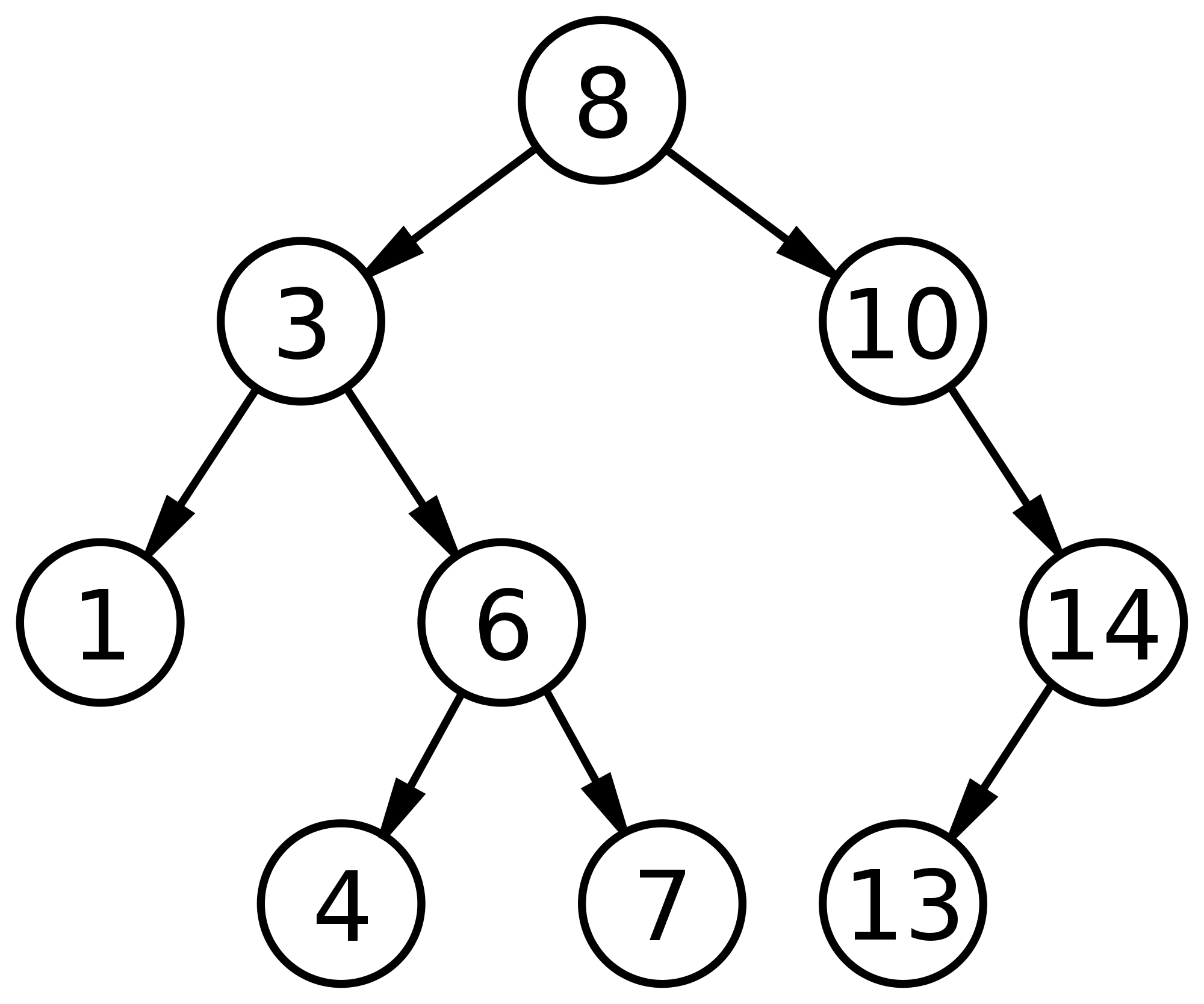
Trees - binary search
Resources
- Khan Academy algorithms course - good review of material in this course
- Code Wars
- Bubble Sort Dance
- Intro to Whiteboarding (Amelia Downs)
- Project Euler - list of mathematical problems
- Practice!